“三维旋转的表示”的版本间的差异
(创建页面,内容为“=== 三维旋转矩阵 === 我们考虑主动旋转,并且通过$$\vec{r} = R\vec{r}$$定义相应的旋转矩阵$$R$$,其中$$r = (x,y,z)^T$$,于是绕固定…”) |
|||
| (未显示同一用户的18个中间版本) | |||
| 第1行: | 第1行: | ||
=== 三维旋转矩阵 === | === 三维旋转矩阵 === | ||
我们考虑主动旋转,并且通过$$\vec{r} = R\vec{r}$$定义相应的旋转矩阵$$R$$,其中$$r = (x,y,z)^T$$,于是绕固定轴(世界轴)XYZ(extrinsic rotations)的旋转矩阵$$R$$为 | 我们考虑主动旋转,并且通过$$\vec{r} = R\vec{r}$$定义相应的旋转矩阵$$R$$,其中$$\vec{r} = (x,y,z)^T$$,于是绕固定轴(世界轴)XYZ(extrinsic rotations)的旋转矩阵$$R$$为 | ||
$$ | $$ | ||
R(\ | R(\varphi,X) = | ||
\begin{pmatrix} \cos(\ | \begin{pmatrix} 1&0&0 \\ 0&\cos(\varphi) & -\sin(\varphi) \\ 0& \sin(\varphi) & \cos(\varphi) | ||
\end{pmatrix}, | |||
R(\varphi,Y) = | |||
\begin{pmatrix} \cos(\varphi)&0&\sin(\varphi) \\ 0&1&0 \\ -\sin(\varphi)&0&\cos(\varphi) | |||
\end{pmatrix}, | |||
R(\varphi,Z) = | |||
\begin{pmatrix} \cos(\varphi) & -\sin(\varphi) & 0 \\ \sin(\varphi) & \cos(\varphi) & 0 \\ 0 & 0 & 1 | |||
\end{pmatrix} | \end{pmatrix} | ||
$$ | $$ | ||
于是连续两次绕世界轴旋转的旋转$$(Z(\varphi)-X(\theta))$$的旋转矩阵为$$R(\theta,X)R(\varphi,Z)$$ | |||
在ROOT中,TRotation类用来描述主动转动的旋转矩阵<code>(TRotation class specifies the rotation of the object in the original system (an active rotation))</code>,与上文的定义一致,使用方法如下 | |||
<syntaxhighlight lang="cpp" line="1"> | |||
TRotation r; | |||
//令r为绕轴TVector3(3,4,5)旋转Pi/3的旋转矩阵 | |||
r.Rotate(TMath::Pi()/3,TVector3(3,4,5)); | |||
//对向量v进行旋转r | |||
TVector3 v; | |||
TRotation r; | |||
v.Transform(r); | |||
v *= r; //Attention v = r * v | |||
//变为恒等变换 | |||
r.SetToIdentity(); | |||
//得到绕固定轴Z旋转phi,再绕固定轴X旋转theta的旋转矩阵 | |||
r.RotateZ(phi) | |||
r.RotateX(theta) | |||
</syntaxhighlight> | |||
===通过欧拉角表示三维旋转=== | |||
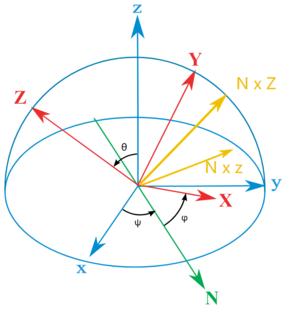
[[文件:EulerAngle.png|缩略图|欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$]] | |||
[[文件:EulerAngle ZXZ.gif|缩略图|欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$动图]] | |||
<!-- | |||
{{multiple image | |||
| width1 = 170 | |||
| footer = Any target orientation can be reached, starting from a known reference orientation, using a specific sequence of intrinsic rotations, whose magnitudes are the Euler angles of the target orientation. This example uses the ''z-x′-z″'' sequence. | |||
| image1 = euler2a.gif | |||
| alt1 = | |||
| width2 = 150 | |||
| image2 = intermediateframes.svg | |||
| alt2 = | |||
| caption2 = | |||
}} | |||
--> | |||
考虑刚体的旋转时,我们取初始的刚体轴作为固定的世界轴 | |||
考虑内旋(intrinsic rotations)定义下(即绕刚体轴旋转)的$$Z(\psi)-X'(\theta)-Z''(\varphi)$$欧拉角旋转,依次旋转的角度为$$\psi,\theta,\varphi$$,它与外旋(extrinsic rotations)定义下(即绕世界轴旋转)的欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$的旋转效果相同,旋转矩阵均为'' | |||
$$ | $$ | ||
R_{ZX'Z''}(\psi,\theta,\varphi) = R_{ZXZ}(\varphi,\theta,\psi) = R(\psi,Z)R(\theta,X)R(\varphi,Z)'' | |||
$$ | $$ | ||
在ROOT中构建欧拉角旋转的旋转矩阵 | |||
\ | <syntaxhighlight lang="cpp" line="1"> | ||
//////////////////////////////////////////////////////////////////////////////// | |||
/// Rotate using the x-convention. | |||
TRotation & TRotation::RotateXEulerAngles(Double_t phi, | |||
Double_t theta, | |||
Double_t psi) { | |||
TRotation euler; | |||
euler.SetXEulerAngles(phi,theta,psi); | |||
return Transform(euler); | |||
} | |||
//////////////////////////////////////////////////////////////////////////////// | |||
/// Rotate using the x-convention (Landau and Lifshitz, Goldstein, &c) by | |||
/// doing the explicit rotations. This is slightly less efficient than | |||
/// directly applying the rotation, but makes the code much clearer. My | |||
/// presumption is that this code is not going to be a speed bottle neck. | |||
TRotation & TRotation::SetXEulerAngles(Double_t phi, | |||
Double_t theta, | |||
Double_t psi) { | |||
SetToIdentity(); | |||
RotateZ(phi); | |||
RotateX(theta); | |||
RotateZ(psi); | |||
return *this; | |||
} | |||
///得到一个(Z(phi)-X(theta)-Z(psi))的外旋欧拉角旋转(extrinsic rotations)的旋转矩阵,即(Z(psi)-X'(theta)-Z''(phi))内旋欧拉角旋转(ntrinsic rotations) | |||
TRotation r; | |||
r.SetXEulerAngles(phi,theta,psi); | |||
</syntaxhighlight> | |||
====例子与ROOT代码验证==== | |||
我们考虑沿`X`轴的单位矢量$$\hat{\vec{x}}$$,即<code>TVector3(1,0,0)</code>,经过欧拉角$$(Z(30^{\circ})-X'(45^{\circ})-Z''(60^{\circ}))$$旋转后的坐标,即上文中令$$\psi=\frac{\pi}{6},\theta=\frac{\pi}{4},\varphi=\frac{\pi}{3}$$。 | |||
几何计算可得坐标为$$(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4\sqrt{2}},\frac{1}{4}+\frac{3}{4\sqrt{2}},\frac{\sqrt{3}}{2\sqrt{2}})\approx(0.13,0.78,0.61)$$ | |||
使用ROOT代码验证(两种方法+一种错误使用) | |||
注:在TRotation的文档里有这么一句 | |||
<code>With a minor caveat, the Euler angles of the rotation may be set using SetXEulerAngles() or individually set with SetXPhi(), SetXTheta(), and SetXPsi(). These routines set the Euler angles using the X-convention which is defined by a rotation about the Z-axis, about the new X-axis, and about the new Z-axis. This is the convention used in Landau and Lifshitz, Goldstein and other common physics texts. </code> | |||
这很容易让人困惑,因为SetXEulerAngles(phi,theta,psi)并不是如文档所说的按新的轴一次转phi,theta,psi,而是按固定轴依次转phi,theta,psi;另外,通过依次SetXPhi(), SetXTheta(), and SetXPsi()并不能正确的实现欧拉角旋转。下面验证这两件事。 | |||
<syntaxhighlight lang="cpp" line="1"> | |||
TRotation R; | |||
R.SetXEulerAngles(TMath::Pi()/3,TMath::Pi()/4,TMath::Pi()/6); | |||
r = TVector3(1,0,0); | |||
(R*r).Print()//并不会改变r的值 | |||
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.780330,0.612372) | |||
//错误的示范 | |||
TRotation R2; | |||
R2.SetXEulerAngles(TMath::Pi()/6,TMath::Pi()/4,TMath::Pi()/3); | |||
(R2*r).Print() | |||
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.926777,0.353553) | |||
//另一种方式 | |||
TVector3 Z(0,0,1); | |||
TVector3 X(1,0,0); | |||
r = TVector3(1,0,0); | |||
r.Rotate(TMath::Pi()/6,Z);//会改变r的值 | |||
X.Rotate(TMath::Pi()/6,Z); | |||
r.Rotate(TMath::Pi()/4,X); | |||
Z.Rotate(TMath::Pi()/4,X); | |||
r.Rotate(TMath::Pi()/3,Z); | |||
r.Print() | |||
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.780330,0.612372) | |||
//通过文档所说的`SetXPhi(), SetXTheta(), and SetXPsi()`来进行欧拉角旋转,会得到错误的结果 | |||
root [13] TRotation R; | |||
root [14] R.SetToIdentity();R.SetXPhi(TMath::Pi()/6);R.SetXTheta(TMath::Pi()/4);R.SetXPsi(TMath::Pi()/3);(R*TVector3(1,0,0)).Print() | |||
TVector3 A 3D physics vector (x,y,z)=(0.324469,0.928023,0.183013) (rho,theta,phi)=(1.000000,79.454709,70.728583) | |||
root [17] R.SetToIdentity();R.SetXPhi(TMath::Pi()/3);R.SetXTheta(TMath::Pi()/4);R.SetXPsi(TMath::Pi()/6);(R*TVector3(1,0,0)).Print() | |||
TVector3 A 3D physics vector (x,y,z)=(0.573223,0.739199,0.353553) (rho,theta,phi)=(1.000000,69.295189,52.207654) | |||
//均不能得到满意的结果,检查SetXPhi()的源代码可以发现,它调用了GetXPhi()等函数,但GetXPhi()并不是一个定义良好的函数,比如: | |||
root [0] TRotation R | |||
(TRotation &) Name: TRotation Title: Rotations of TVector3 objects | |||
root [1] R.SetXPhi(TMath::Pi()/3) | |||
root [2] R.GetXPhi() | |||
(double) 0.52359878 | |||
root [3] R.SetXTheta(0) | |||
root [4] R.SetXPsi(0) | |||
root [5] R.GetXPhi() | |||
(double) 0.26179939 | |||
root [6] R.GetXTheta() | |||
(double) 0.0000000 | |||
root [7] R.GetXPhi() | |||
(double) 0.26179939 | |||
//这也许是SetXPhi(), SetXTheta(), and SetXPsi()不能正常使用的原因 | |||
</syntaxhighlight> | |||
=== 三维旋转+平移 === | |||
描述刚体的空间变换,需要有一个初始刚体和变换后的刚体,选择初始刚体位于世界坐标系中心,刚体自身坐标系与世界坐标系重合,然后来描述末态刚体相对初始刚体的几何变换。这可以通过先旋转后平移来描述,设末态刚体某点坐标为$$\vec{r}$$,则$$\vec{r}=R\vec{r}_0+\vec{d}$$,其中$$\vec{d}$$为末态刚体的坐标系中心相对初始刚体坐标系中心的位矢, $$R$$为将末态刚体平移至使得其自身坐标系中心和初态刚体的坐标系中心重合后,相对于初态刚体的旋转矩阵。 | |||
2022年2月24日 (四) 16:52的最新版本
三维旋转矩阵
我们考虑主动旋转,并且通过$$\vec{r} = R\vec{r}$$定义相应的旋转矩阵$$R$$,其中$$\vec{r} = (x,y,z)^T$$,于是绕固定轴(世界轴)XYZ(extrinsic rotations)的旋转矩阵$$R$$为
$$ R(\varphi,X) = \begin{pmatrix} 1&0&0 \\ 0&\cos(\varphi) & -\sin(\varphi) \\ 0& \sin(\varphi) & \cos(\varphi) \end{pmatrix}, R(\varphi,Y) = \begin{pmatrix} \cos(\varphi)&0&\sin(\varphi) \\ 0&1&0 \\ -\sin(\varphi)&0&\cos(\varphi) \end{pmatrix}, R(\varphi,Z) = \begin{pmatrix} \cos(\varphi) & -\sin(\varphi) & 0 \\ \sin(\varphi) & \cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
于是连续两次绕世界轴旋转的旋转$$(Z(\varphi)-X(\theta))$$的旋转矩阵为$$R(\theta,X)R(\varphi,Z)$$
在ROOT中,TRotation类用来描述主动转动的旋转矩阵(TRotation class specifies the rotation of the object in the original system (an active rotation)),与上文的定义一致,使用方法如下
TRotation r;
//令r为绕轴TVector3(3,4,5)旋转Pi/3的旋转矩阵
r.Rotate(TMath::Pi()/3,TVector3(3,4,5));
//对向量v进行旋转r
TVector3 v;
TRotation r;
v.Transform(r);
v *= r; //Attention v = r * v
//变为恒等变换
r.SetToIdentity();
//得到绕固定轴Z旋转phi,再绕固定轴X旋转theta的旋转矩阵
r.RotateZ(phi)
r.RotateX(theta)
通过欧拉角表示三维旋转
考虑刚体的旋转时,我们取初始的刚体轴作为固定的世界轴
考虑内旋(intrinsic rotations)定义下(即绕刚体轴旋转)的$$Z(\psi)-X'(\theta)-Z''(\varphi)$$欧拉角旋转,依次旋转的角度为$$\psi,\theta,\varphi$$,它与外旋(extrinsic rotations)定义下(即绕世界轴旋转)的欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$的旋转效果相同,旋转矩阵均为 $$ R_{ZX'Z''}(\psi,\theta,\varphi) = R_{ZXZ}(\varphi,\theta,\psi) = R(\psi,Z)R(\theta,X)R(\varphi,Z)'' $$
在ROOT中构建欧拉角旋转的旋转矩阵
////////////////////////////////////////////////////////////////////////////////
/// Rotate using the x-convention.
TRotation & TRotation::RotateXEulerAngles(Double_t phi,
Double_t theta,
Double_t psi) {
TRotation euler;
euler.SetXEulerAngles(phi,theta,psi);
return Transform(euler);
}
////////////////////////////////////////////////////////////////////////////////
/// Rotate using the x-convention (Landau and Lifshitz, Goldstein, &c) by
/// doing the explicit rotations. This is slightly less efficient than
/// directly applying the rotation, but makes the code much clearer. My
/// presumption is that this code is not going to be a speed bottle neck.
TRotation & TRotation::SetXEulerAngles(Double_t phi,
Double_t theta,
Double_t psi) {
SetToIdentity();
RotateZ(phi);
RotateX(theta);
RotateZ(psi);
return *this;
}
///得到一个(Z(phi)-X(theta)-Z(psi))的外旋欧拉角旋转(extrinsic rotations)的旋转矩阵,即(Z(psi)-X'(theta)-Z''(phi))内旋欧拉角旋转(ntrinsic rotations)
TRotation r;
r.SetXEulerAngles(phi,theta,psi);
例子与ROOT代码验证
我们考虑沿`X`轴的单位矢量$$\hat{\vec{x}}$$,即TVector3(1,0,0),经过欧拉角$$(Z(30^{\circ})-X'(45^{\circ})-Z''(60^{\circ}))$$旋转后的坐标,即上文中令$$\psi=\frac{\pi}{6},\theta=\frac{\pi}{4},\varphi=\frac{\pi}{3}$$。
几何计算可得坐标为$$(\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4\sqrt{2}},\frac{1}{4}+\frac{3}{4\sqrt{2}},\frac{\sqrt{3}}{2\sqrt{2}})\approx(0.13,0.78,0.61)$$
使用ROOT代码验证(两种方法+一种错误使用)
注:在TRotation的文档里有这么一句
With a minor caveat, the Euler angles of the rotation may be set using SetXEulerAngles() or individually set with SetXPhi(), SetXTheta(), and SetXPsi(). These routines set the Euler angles using the X-convention which is defined by a rotation about the Z-axis, about the new X-axis, and about the new Z-axis. This is the convention used in Landau and Lifshitz, Goldstein and other common physics texts.
这很容易让人困惑,因为SetXEulerAngles(phi,theta,psi)并不是如文档所说的按新的轴一次转phi,theta,psi,而是按固定轴依次转phi,theta,psi;另外,通过依次SetXPhi(), SetXTheta(), and SetXPsi()并不能正确的实现欧拉角旋转。下面验证这两件事。
TRotation R;
R.SetXEulerAngles(TMath::Pi()/3,TMath::Pi()/4,TMath::Pi()/6);
r = TVector3(1,0,0);
(R*r).Print()//并不会改变r的值
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.780330,0.612372)
//错误的示范
TRotation R2;
R2.SetXEulerAngles(TMath::Pi()/6,TMath::Pi()/4,TMath::Pi()/3);
(R2*r).Print()
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.926777,0.353553)
//另一种方式
TVector3 Z(0,0,1);
TVector3 X(1,0,0);
r = TVector3(1,0,0);
r.Rotate(TMath::Pi()/6,Z);//会改变r的值
X.Rotate(TMath::Pi()/6,Z);
r.Rotate(TMath::Pi()/4,X);
Z.Rotate(TMath::Pi()/4,X);
r.Rotate(TMath::Pi()/3,Z);
r.Print()
//输出TVector3 A 3D physics vector (x,y,z)=(0.126826,0.780330,0.612372)
//通过文档所说的`SetXPhi(), SetXTheta(), and SetXPsi()`来进行欧拉角旋转,会得到错误的结果
root [13] TRotation R;
root [14] R.SetToIdentity();R.SetXPhi(TMath::Pi()/6);R.SetXTheta(TMath::Pi()/4);R.SetXPsi(TMath::Pi()/3);(R*TVector3(1,0,0)).Print()
TVector3 A 3D physics vector (x,y,z)=(0.324469,0.928023,0.183013) (rho,theta,phi)=(1.000000,79.454709,70.728583)
root [17] R.SetToIdentity();R.SetXPhi(TMath::Pi()/3);R.SetXTheta(TMath::Pi()/4);R.SetXPsi(TMath::Pi()/6);(R*TVector3(1,0,0)).Print()
TVector3 A 3D physics vector (x,y,z)=(0.573223,0.739199,0.353553) (rho,theta,phi)=(1.000000,69.295189,52.207654)
//均不能得到满意的结果,检查SetXPhi()的源代码可以发现,它调用了GetXPhi()等函数,但GetXPhi()并不是一个定义良好的函数,比如:
root [0] TRotation R
(TRotation &) Name: TRotation Title: Rotations of TVector3 objects
root [1] R.SetXPhi(TMath::Pi()/3)
root [2] R.GetXPhi()
(double) 0.52359878
root [3] R.SetXTheta(0)
root [4] R.SetXPsi(0)
root [5] R.GetXPhi()
(double) 0.26179939
root [6] R.GetXTheta()
(double) 0.0000000
root [7] R.GetXPhi()
(double) 0.26179939
//这也许是SetXPhi(), SetXTheta(), and SetXPsi()不能正常使用的原因
三维旋转+平移
描述刚体的空间变换,需要有一个初始刚体和变换后的刚体,选择初始刚体位于世界坐标系中心,刚体自身坐标系与世界坐标系重合,然后来描述末态刚体相对初始刚体的几何变换。这可以通过先旋转后平移来描述,设末态刚体某点坐标为$$\vec{r}$$,则$$\vec{r}=R\vec{r}_0+\vec{d}$$,其中$$\vec{d}$$为末态刚体的坐标系中心相对初始刚体坐标系中心的位矢, $$R$$为将末态刚体平移至使得其自身坐标系中心和初态刚体的坐标系中心重合后,相对于初态刚体的旋转矩阵。