三维旋转的表示

三维旋转矩阵

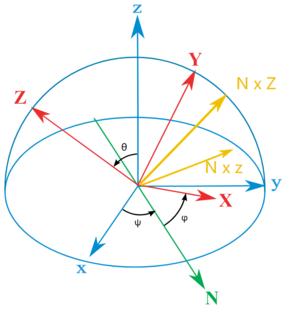
我们考虑主动旋转，并且通过$$\vec{r} = R\vec{r}$$定义相应的旋转矩阵$$R$$，其中$$\vec{r} = (x,y,z)^T$$，于是绕固定轴（世界轴）XYZ(extrinsic rotations)的旋转矩阵$$R$$为

$$ R(\varphi,X) = \begin{pmatrix} 1&0&0 \\ 0&\cos(\varphi) & -\sin(\varphi) \\ 0& \sin(\varphi) & \cos(\varphi) \end{pmatrix}, R(\varphi,Y) = \begin{pmatrix} \cos(\varphi)&0&\sin(\varphi) \\ 0&1&0 \\ -\sin(\varphi)&0&\cos(\varphi) \end{pmatrix}, R(\varphi,Z) = \begin{pmatrix} \cos(\varphi) & -\sin(\varphi) & 0 \\ \sin(\varphi) & \cos(\varphi) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

于是连续两次绕世界轴旋转的旋转$$(Z(\varphi)-X(\theta))$$的旋转矩阵为$$R(\theta,X)R(\varphi,Z)$$

在ROOT中，TRotation类用来描述主动转动的旋转矩阵(TRotation class specifies the rotation of the object in the original system (an active rotation))，与上文的定义一致，使用方法如下

TRotation r; 
//令r为绕轴TVector3(3,4,5)旋转Pi/3的旋转矩阵
r.Rotate(TMath::Pi()/3,TVector3(3,4,5));
//对向量v进行旋转r
TVector3 v;
TRotation r;
v.Transform(r);
v *= r;  //Attention v = r * v
//变为恒等变换
r.SetToIdentity();
//得到绕固定轴Z旋转phi,再绕固定轴X旋转theta的旋转矩阵
r.RotateZ(phi)
r.RotateX(theta)

通过欧拉角表示三维旋转

欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$

欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$动图

考虑内旋(intrinsic rotations)定义下（即绕刚体轴旋转）的$$Z(\psi)-X'(\theta)-Z''(\varphi)$$欧拉角旋转，依次旋转的角度为$$\psi,\theta,\varphi$$,它与外旋(extrinsic rotations)定义下（即绕世界轴旋转）的欧拉角$$Z(\varphi)-X(\theta)-Z(\psi)$$的旋转效果相同，旋转矩阵均为 $$ R_{ZX'Z''}(\psi,\theta,\varphi) = R_{ZXZ}(\varphi,\theta,\psi) = R(\psi,Z)R(\theta,X)R(\varphi,Z)'' $$

在ROOT中构建欧拉角旋转的旋转矩阵

////////////////////////////////////////////////////////////////////////////////
/// Rotate using the x-convention.
 
TRotation & TRotation::RotateXEulerAngles(Double_t phi,
                                         Double_t theta,
                                         Double_t psi) {
   TRotation euler;
   euler.SetXEulerAngles(phi,theta,psi);
   return Transform(euler);
}

////////////////////////////////////////////////////////////////////////////////
/// Rotate using the x-convention (Landau and Lifshitz, Goldstein, &c) by
/// doing the explicit rotations.  This is slightly less efficient than
/// directly applying the rotation, but makes the code much clearer.  My
/// presumption is that this code is not going to be a speed bottle neck.
 
TRotation & TRotation::SetXEulerAngles(Double_t phi,
                                      Double_t theta,
                                      Double_t psi) {
   SetToIdentity();
   RotateZ(phi);
   RotateX(theta);
   RotateZ(psi);
 
   return *this;
}

///得到一个(Z(phi)-X(theta)-Z(psi))的外旋欧拉角旋转(extrinsic rotations)的旋转矩阵，即(Z(psi)-X'(theta)-Z''(phi))内旋欧拉角旋转(ntrinsic rotations)

TRotation r;
r.SetXEulerAngles(phi,theta,psi);